KvG-Mathiade 2002
Die Aufgaben der 1. Runde
Jahrgangsstufe 5-6: Streichholzspiele
Mit Streichhölzern kannst du Feuer, aber auch ganz andere Dinge machen. Zum Beispiel kannst du 24 Hölzchen so auf den Tisch legen (s. rechts).1) Wie viele Quadrate enthält die Figur?
2) Stelle dir vor, du möchtest von den vorhandenen neun Quadraten mit je 1 Streichholz Seitenlänge genau fünf übrigbehalten. Wie viele Streichhölzer musst du dazu mindestens, wie viele kannst du höchstens wegnehmen?
3) Nimm aus der Figur oben acht Streichhölzer so weg, dass genau 2 (3, 4, 5, 6) Quadrate übrigbleiben. Die Quadrate dürfen bei dieser Teilaufgabe unterschiedlich groß sein und auch ineinander liegen oder übereinander greifen.
Zeichne zu den Aufgabenteilen 2) und 3) die Lösungsfiguren auf und beschreibe, wie du überlegt hast!Jahrgangsstufen 7-9: Merkwürdige Aussteiger!
Der Linienbus ist auf dem Weg zur Endstation; an den letzten sechs Haltestellen steigt niemand mehr ein. Nur "Aussteiger" gibt es noch, nämlich an der sechstletzten Station ein Achtel der Fahrgäste minus ¾ Personen, an der fünftletzten die Hälfte der dann noch Anwesenden minus 1½ Personen und an der viertletzten zwei Drittel der übrigen Fahrgäste plus
Person. Beim nächsten Mal steigen von dem Rest wieder die Hälfte plus ½ Person aus und dann von den Verbleibenden die Hälfte minus ½ Person. Nur Asterix und Obelix fahren bis zur Endstation mit. Lösung von Jonas Wieschmann (9a) zur Aufgabe für JgSt. 7-9:x sei die Anzahl der Personen, die sich jeweils an der betreffenden Haltestelle im Bus befanden. |
 |
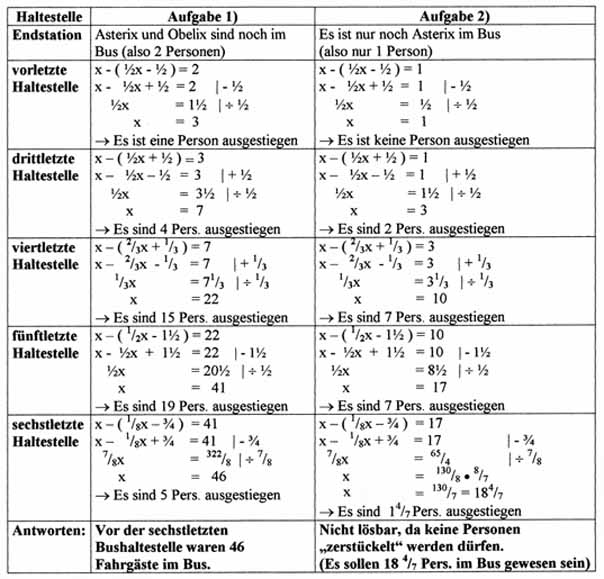2) Wie stellt sich das Problem dar, wenn an der Endstation nur noch Asterix im Bus sitzt?
Gefragt ist nicht nur die Lösung, sondern auch eine Darstellung deines Gedanken- bzw. Rechenganges.
Jahrgangsstufen 10-13: Zahlen als Vorgesetzte
Gesucht sind zwei n-stellige natürliche Zahlen a und b mit den Eigenschaften:a) Die Summe beider Zahlen ist 10n – 1.
b) Setzt man a vor b, so ist die entstehende Zahl k-mal so groß wie die Zahl, die entsteht, wenn man b vor a setzt.
1) Für n = 3 und k = 6 lautet Bedingung a): a + b = 999. Stelle für diesen Fall auch eine Gleichung zu b) auf. Zeige, dass dann das Problem lösbar ist. Wie lauten die Zahlen a und b?
2) Verallgemeinere deinen Ansatz und zeige, dass das Problem für n = 3 und k ≠ 6 nicht lösbar ist!
3) Zeige, dass die Aufgabe auch für beliebiges n und k ≠ 6 nicht lösbar ist!
4) Höchstens für k = 6 kann also eine Lösung existieren. Suche das kleinste n>3, für das dies der Fall ist! Wie lauten dann die Lösungen a und b?
Die Aufgaben der 2. Runde
Jahrgangsstufen 5-6: Eine Kolonie und ihre Bewohner
 |
|
a) In dem roten Haus wohnt ein Engländer. b) Der Spanier hat einen Hund. c) Im grünen Haus trinkt man Kaffee. d) Tee trinkt der Russe. e) Und links neben dem weißen steht das grüne Haus. f) Der Klavierspieler züchtet Bienen. g) Aus dem gelben Haus erklingt öfters Geigenspiel. h) Der Milchtrinker wohnt genau in der Mitte. i) Der Norweger hingegen wohnt im ersten Haus. j) Der Posaunist ist unmittelbarer Nachbar des Herrn mit der Katze. k) Der Geiger wohnt neben dem Haus mit dem Pferd. l) Der Flötenspieler trinkt übrigens Orangensaft. m) Der Japaner übt fleißig auf seinem Schlagzeug. n) Das Haus des Norwegers steht, um es nicht zu vergessen, neben dem blauen Haus. |
Kannst du alle Häuser mit ihren Farben und Bewohnern sowie deren Haustieren, Instrumenten und Getränken richtig erfassen? Übrigens: Wer trinkt Wasser? Und wem gehört eigentlich das Zebra?
Jahrgangsstufen 7-9: Geklaute Nüsse
A-Hörnchen war fleißig: Für den Winter hat es viele Nüsse gesammelt, die es in seiner Höhle versteckt hat. B-Hörnchen, auch nicht faul, hat dieses Versteck aufgestöbert und nimmt die Hälfte der Nüsse weg. "Wenn ich noch 10 Nüsse mehr wegnehme, wird das wohl auch noch nicht auffallen," denkt B-Hörnchen. Gesagt, getan! Aber nicht genug: Der Reiz des "Klauens" ist einmal da, die Angstschwelle überwunden, und so nimmt B-Hörnchen von dem Rest abermals die Hälfte und anschließend dann noch einmal 4 Nüsse weg.Erst die Freude, nicht erwischt zu werden, dann das Nachdenken, dann die Reue: "So ganz in Ordnung war die Klauerei ja nicht," ist B-Hörnchens Einsicht am nächsten Tag, "ich muss den Fehler wohl wieder gutmachen!" Also, wie war das noch? "10 Nüsse muss A-Hörnchen zurückbekommen, dann wird die Anzahl der vorhandenen Nüsse verdoppelt, dann kommen 4 Nüsse dazu, dann verdoppele ich wieder die Anzahl ," denkt sich B-Hörnchen und verfährt so.
Als A-Hörnchen einige Tage später seine Nüsse nachzählt, findet es 108 Stück und ist erstaunt, einige mehr vorzufinden, als es vorher in sein Versteck gelegt hatte. Wie ist das zu erklären? Und wie viele Nüsse hatte A-Hörnchen ursprünglich?
Jahrgangsstufen 10-12: Seltsame Ziffern
Es gilt: 113 = 1, 213 = 8192, 313 = 1594323, 413 = 67108864, ... , 3713 = ....Alle diese Zahlen haben eine gemeinsame Eigenschaft!
1) Beweise, dass für jede natürliche Zahl n die Einerziffer von n13 mit der Einerziffer von n übereinstimmt!
2) Beweise, dass die gleiche Eigenschaft auch auf n25 und n49zutrifft!
3) Auf welche Potenzen von n trifft die Eigenschaft außerdem noch zu? Verallgemeinere und beweise! (Vielleicht kann eine binomische Formel dir weiterhelfen!)
Preisverleihung zum Mathe-Wettbewerb Känguru 2002
|
|||
|
|||
|
Rauchende Köpfe am KvG: Mathe-Wettbewerb Känguru
|
|
