KvG-Mathiade 2001

Die Aufgaben der 1. Runde

Jahrgangsstufe 5-6: Eine spannende Indianergeschichte

Hätte Häuptling „Langes Rechteck“ vom Stamme der Lotpunktfuß-Indianer nicht Geburtstag – vielleicht wäre es dann den vier gefangenen Bleichgesichtern schlecht ergangen. So aber gibt er ihnen großmütig eine Chance: „Ich habe hier drei weiße und vier schwarze Federn. Jedem von euch wird jetzt eine davon an den Skalp gesteckt, nachdem ihr euch auf diesen Baumstamm gesetzt habt. Nun kann jeder eine Aussage über die Feder auf seinem Kopf machen, sie kann lauten: „schwarz“, „weiß“ oder „ich weiß es nicht“. Wenn dabei niemand eine falsche Farbe und wenigstens einer die richtige Farbe angibt, so schenke ich euch die Freiheit, andernfalls wartet auf euch der Marterpfahl!“
Die vier Gefangenen beratschlagen kurz. Was sollen sie tun? Die Feder auf seinem eigenen Kopf wird man nicht sehen können, nur die Federn seiner Vorderleute, denn auch Umdrehen ist verboten! Nennt nur einer eine falsche Farbe, so sind alle vier verloren. Dass alle vier „ich weiß es nicht“ sagen, ist natürlich auch nicht möglich, denn wenigstens einer soll ja seine Farbe richtig nennen. Soll man raten - oder: Kannst du eine sichere Methode angeben, mit der die vier freikommen? Bitte beschreibe und begründe sie ausführlich!

Jahrgangsstufe 7-9: Seltsame Zwillinge

a) Wenn man eine dreistellige Zahl zweimal hintereinander schreibt, entsteht eine „Zwillingszahl“. Aus 537 entsteht z. B. die Zwillingszahl 537537, aus 221 die Zwillingszahl 221221.
Beweise, dass solche Zwillingszahlen immer durch 13 teilbar sind.

b) „Primzahlzwillinge“ sind Primzahlen, deren Differenz 2 ist, z. B. 17 und 19, 29 und 31, 59 und 61, 101 und 103.
Beweise: Die Summe zweier Primzahlzwillinge, die größer als 3 sind (z. B. 17 + 19 = 36), ist stets durch 12 teilbar. (Anmerkung: „Teilbarkeit“ bedeutet, dass das Ergebnis der Division ganzzahlig ist!)

Jahrgangsstufe 10-13: Ein besonderes Rechteck

Das abgebildete Rechteck mit der Länge 12 cm hat eine besondere Eigenschaft: Zwei gleichgroße Kreise lassen sich - wie dargestellt - so einzeichnen, dass jeder von ihnen eine Diagonale, eine Mittellinie und zwei Seiten berührt. Berechne mit Hilfe dieser Angaben die Rechtecksbreite x!

Die Aufgaben der 2. Runde

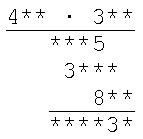
Jahrgangsstufe 5-6: Multiplikation mit Lücken

"Kryptogramme" nennt man Aufgaben wie diese, in der verborgene Ziffern vorkommen.
Die Sternchen sind so durch Ziffern zu ersetzen, dass eine richtig gelöste Multiplikationsaufgabe entsteht. Dabei muss jede Zahl mit einer von Null verschiedenen Ziffer beginnen.

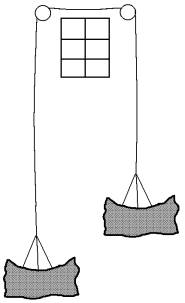
Jahrgangsstufe 7-9: Eine schwierige Rettungsaktion

Lang, lang ist’s her: Ein altes Rettungssystem für Hotels bei Brandgefahr bestand aus einem Seil mit zwei Körben an den Enden. Das Seil wurde über Rollen geführt, die oberhalb eines Hotelfensters befestigt waren.
Wurde ein Korb heruntergelassen, so fuhr der andere Korb gleichzeitig hoch. Der Inhalt eines Korbes durfte dabei höchstens 15 kg schwerer sein als der des anderen, damit man den Gewichtsunterschied durch Ziehen bzw. Festhalten ausgleichen konnte.
Das bedeutet: Alles, was bis zu 15 kg wog, konnte ohne Beladung des "Gegenkorbes" befördert werden. War ein Korb beladen, so konnte man in dem anderen eine um bis zu 15 kg leichtere oder schwerere Last (aus einer oder mehreren Personen) transportieren.
Maja Mathefix, die eine Beschreibung dieses Rettungssystems in einem Abenteuerbuch gefunden hatte, überlegt nun: Wären mein Vater (105 kg !!), meine Mutter (45 kg), mein kleines Brüderchen (15 kg) und unser Hund (30 kg) in diesem Hotel und wären auch keine Helfer anwesend - könnten sie sich dann bei Brandgefahr durch besagten "Fahrkorb" retten?
Erschwerend kommt hinzu, dass Baby und Hund den Korb ohne Hilfe nicht besteigen oder verlassen können. Da ist es immerhin tröstlich, dass die Konstruktion so stark ist, dass jeder Korb zur Not alle Personen und den Hund auf einmal aufnehmen kann.
Nach langer Überlegung findet Maja schließlich eine Lösung. Schaffst du es auch?

Jahrgangsstufe 10 -13: Aufeinanderfolgende Zahlen

Schule vor mehr als zweihundert Jahren: Um seine Schüler zu beschäftigen, stellte der Lehrer ihnen die Aufgabe, alle ganzen Zahlen von 1 bis 100 zu addieren. Er glaubte nun, für eine ganze Stunde Ruhe zum Korrigieren von Arbeiten zu haben, zumal die Schreibarbeit mit Griffeln auf Schiefertafeln eine recht umständliche Prozedur war. Überraschenderweise meldete sich aber schon nach fünf Minuten der 7-jährige Friedrich mit dem richtigen Ergebnis: "Du hast ja nur eine Rechnung auf der Tafel, aber sie stimmt!" staunte der Lehrer.
Friedrich war der junge Carl Friedrich Gauß (1777-1855), einer der berühmtesten Mathematiker, dessen Porträt übrigens auf jedem Zehnmarkschein zu finden ist. Er hatte so gerechnet: 1 + ... + 100 = (1+100) + (2+99) + ... + (50+51) = 50 ∙ 101 = 5050.
a) Verallgemeinere diese Rechnung und zeige für jede natürliche Zahl k: .
b) Zeige: Eine Summe dreier aufeinanderfolgender Zahlen ist immer durch 3 teilbar. (Tipp: n +...+... = ? )
c) Formuliere einen entsprechenden Satz für fünf aufeinanderfolgende Zahlen und beweise ihn!
d) Zeige, dass dieser Satz auch für jede ungerade Anzahl k aufeinanderfolgender Zahlen gilt.
e) Was lässt sich über gerade Anzahlen aufeinanderfolgender Zahlen sagen?