KvG-Mathiade 2000

Die Aufgaben der 1. Runde

Jahrgangsstufe 5-7: Ein neues Rechenverfahren!

Manni Mathefix hat ein neues Verfahren für die schriftliche Multiplikation entwickelt; hier wird es anhand zweier Beispiele vorgestellt.

a) Formuliere eine Anleitung für dieses Rechenverfahren! Sie muss so genau sein, dass jemand, der es nicht kennt, es daraus erlernen kann.
b) Berechne nach dem Verfahren die Aufgabe 76 · 23.
c) Begründe möglichst ausführlich, warum das Verfahren zum richtigen Ergebnis führt.

Jahrgangsstufe 8-9: Sind alle Dreiecke gleichschenklig?

	Preisverleihung 2000

Es gibt ganz verrückte Dreiecke: rechtwinklige, stumpfwinklige, spitzwinklige, mit verschieden langen Seiten und unterschiedlichen Winkeln... Aber: Was soll‘s? Detlef Denknix, der große Logiker, behauptet steif und fest: "Ich kann jedes Dreieck gleichschenklig machen." Und er hat sich auch einen Beweis dafür ausgedacht - mit Planskizze, wie sich das für einen geometrischen Beweis gehört. Dazu hat er sich überlegt:
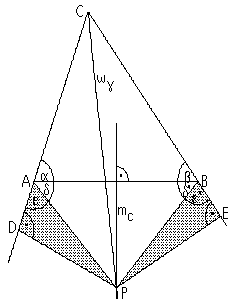
„Gegeben sei ein beliebiges Dreieck ABC. Wenn es schon gleichschenklig ist, so habe ich nichts mehr zu tun. Falls noch nicht, so sind die Winkelhalbierende w_γ und die Mittelsenkrechte m_c voneinander verschieden und haben einen Schnittpunkt P. Ich verbinde P mit A und B und zeichne außerdem die Senkrechten zu den Seitengeraden AC und CB durch P; die Fußpunkte nenne ich D und E (s. Zeichnung). Nun gilt:

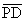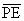1) und sind gleichlang, weil P auf w_γ liegt.
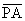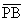2) und sind gleichlang, weil P auf m_c liegt.
3) Dreieck PAD und Dreieck EBP sind nach dem Kongruenzsatz Ssw kongruent, weil sie in dem rechten Winkel, einer anliegenden Seite (s. 1) und der gegenüberliegenden Seite (s. 2) übereinstimmen.
4) ε = ε' als entsprechende Stücke in kongruenten Dreiecken (s. 3).
5) δ = δ', weil Δ PAB gleichschenklig ist (s. 2).
6) α = β als Nebenwinkel von ε + δ = ε' + δ' (s. 4 und 5).
7) Δ ABC ist gleichschenklig, weil die Basiswinkel α und β gleichgroß sind (s. 6)."

Da bekanntlich nicht jedes Dreieck gleichschenklig ist, muss Detlefs Überlegung einen Fehler enthalten. In welchem Schritt (von 1 bis 7) steckt dieser Fehler, und warum? Bitte formuliere deine Lösung möglichst genau und ausführlich. Hinweise wie "Das sieht man doch, dass Δ ABC nicht gleichschenklig ist" reichen nicht aus!

Jahrgangsstufe 10 -13: Pythagoreische Tripel

Betrachte die Gleichungen:


a) Wie lauten die Gleichungen 4), 5), 6) und 7)?
b) Formuliere eine möglichst einfache Gleichung mit einer Variablen n, die sich als Verallgemeinerung aus den Gleichungen 1), ..., 7) ergibt!
c) Beweise, dass diese Gleichung für alle natürlichen Zahlen n gilt.

Die Aufgaben der 2. Runde

Jahrgangsstufe 5-7: Wer wird König?

Die Schönheit der Prinzessin war weit über die Grenzen des Landes hinaus berühmt, und viele Prinzen warben um sie. Derjenige sollte sie bekommen, der folgende Aufgabe lösen konnte: „Ich habe hier einen Korb mit Pflaumen. Wenn ich davon dem ersten Prinzen die Hälfte und noch eine Pflaume, dem zweiten die Hälfte des Restes und wiederum dazu eine Pflaume, dem dritten die Hälfte des nunmehrigen Restes und drei Pflaumen gebe, dann ist der Korb geleert. Nenne die Anzahl der Pflaumen, die der Korb enthält!“ Hättest du die Hand der Prinzessin erhalten?

Das mit der Prinzessin ist natürlich nur eine Sage. Anders gesagt: Selbstverständlich ist diese Aufgabe nicht nur für Jungen, sondern auch für Mädchen gedacht!

Jahrgangsstufe 8-9: Katze = Maus?

Auf einer Waage sitzen eine Katze (mit dem Gewicht k) und eine Maus (mit dem Gewicht m). Die Waage zeigt ein Gesamtgewicht von 2 kg.

Manni Mathefix will beweisen, dass Katze und Maus gleich schwer sind; dazu macht er folgende Term- und Gleichungsumformungen: (s. rechts) Also ist k = m, das heißt, Katze und Maus wiegen gleich viel. Oder? Wo liegt der Fehler, und worin besteht er?

Jahrgangsstufe 10-13: Eine besondere Quadratzahl

Gesucht ist das Quadrat x² einer rationalen (d. h. als Bruch mit ganzen Zahlen darstellbaren) Zahl x mit der Eigenschaft, dass
ebenfalls Quadrate rationaler Zahlen sind.

(Tipp: Verwende die Darstellung !)